|
1. Loi normale ou de Gauss
Supposons que nous tirions des échantillons aléatoires d'une population
dont la taille moyenne est de 170 cm,
avec un écart type de 10 cm.
Traçons l'histogramme de la taille, avec des classes de 5 cm de
large, pour des échantillons de plus en plus grands.
Examinons l'aspect de ces histogrammes.
* Pour cette exemple, les classes sont de
2 cm
Au fur et à mesure que la taille de l'échantillon augmente
(et que la taille des classes diminue),
l'histogramme devient de plus en plus régulier et se rapproche d'une courbe
en cloche, appelée loi normale.
Loi normale
Loi normale
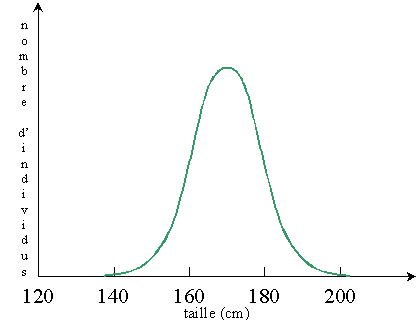
Cette courbe est aussi appelée loi de Gauss,
en l'honneur du grand mathématicien allemand
Karl Friederich Gauss (1777-1855).
La loi normale est la loi statistique la plus
répandue et la plus utile.
Elle représente beaucoup de phénomènes aléatoires.
De plus, de nombreuses autres lois statistiques
peuvent être approchées par la loi normale, tout spécialement dans le
cas des grands échantillons.
Son expression mathématique est la suivante:
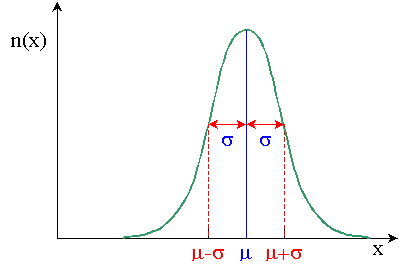
Lorsque la distribution des individus dans une population obéit à la loi
normale, on trouve:
2. Calcul des probabilités
Pour calculer les probabilités associées à la loi normale, on utilise
généralement la loi normale réduite:
c'est une loi normale pour laquelle 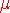 =0 et =0 et
 =1. =1.
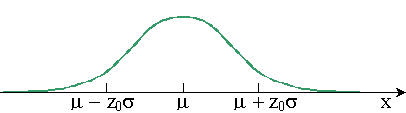
La table suivante permet de déterminer la probabilité que la variable
x s'écarte de la moyenne 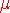 de plus de
z0 × de plus de
z0 ×  vers le haut.
vers le haut.
Pour obtenir z0, on calcule l'écart par rapport à la moyenne:
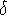 = x - = x - 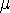 , puis on divise par l'écart type: , puis on divise par l'écart type:
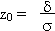
|
2ème décimale de
z0 |
|
Z0 |
|
0 |
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
0.0
0.1
0.2
0.3
0.4 |
.500
.460
.421
.382
.345 |
.496
.456
.417
.378
.341 |
.492
.452
.413
.374
.337 |
.488
.448
.409
.371
.334 |
.484
.444
.405
.367
.330 |
.480
.440
.401
.363
.326 |
.476
.436
.397
.359
.323 |
.472
.433
.394
.356
.319 |
.468
.429
.390
.352
.316 |
.464
.425
.386
.348
.312 |
0.5
0.6
0.7
0.8
0.9 |
.309
.274
.242
.212
.184 |
.305
.271
.239
.209
.181 |
.302
.268
.236
.206
.179 |
.298
.264
.233
.203
.176 |
.295
.261
.230
.200
.174 |
.291
.258
.227
.198
.171 |
.288
.255
.224
.195
.169 |
.284
.251
.221
.192
.166 |
.281
.248
.218
.189
.164 |
.278
.245
.215
.187
.161 |
|
1.0
1.1
1.2
1.3
1.4 |
.159
.136
.115
.097
.081 |
.156
.133
.113
.095
.079 |
.154
.131
.111
.093
.078 |
.152
.129
.109
.092
.076 |
.149
.127
.107
.090
.075 |
.147
.125
.106
.089
.074 |
.145
.123
.104
.087
.072 |
.142
.121
.102
.085
.071 |
.140
.119
.100
.084
.069 |
.138
.117
.099
.082
.068 |
|
1.5
1.6
1.7
1.8
1.9 |
.067
.055
.045
.036
.029 |
.066
.054
.044
.035
.028 |
.064
.053
.043
.034
.027 |
.063
.052
.042
.034
.027 |
.062
.051
.041
.033
.026 |
.061
.049
.040
.032
.026 |
.059
.048
.039
.031
.025 |
.058
.047
.038
.031
.024 |
.057
.046
.038
.030
.024 |
.056
.046
.037
.029
.023 |
|
2.0
2.1
2.2
2.3
2.4 |
.023
.018
.014
.011
.008 |
.022
.017
.014
.010
.008 |
.022
.017
.013
.010
.008 |
.021
.017
.013
.010
.008 |
.021
.016
.013
.010
.007 |
.020
.016
.012
.009
.007 |
.020
.015
.012
.009
.007 |
.019
.015
.012
.009
.007 |
.019
.015
.011
.009
.007 |
.018
.014
.011
.008
.006 |
|
2.5
2.6
2.7
2.8
2.9 |
.006
.005
.003
.003
.002 |
.006
.005
.003
.002
.002 |
.006
.004
.003
.002
.002 |
.006
.004
.003
.002
.002 |
.006
.004
.003
.002
.002 |
.005
.004
.003
.002
.002 |
.005
.004
.003
.002
.002 |
.005
.004
.003
.002
.001 |
.005
.004
.003
.002
.001 |
.005
.004
.003
.002
.001 |
Cette probabilité peut aussi être calculée à l'aide de formules
approximatives, plus aisées à manipuler. L'une d'elles est implémentée
ci-dessous. Sa précision est très bonne (l'erreur est au maximum de
0,000015).
N.B.: Les probabilités inférieures à
10-10 = 10e-10 (un dix milliardième) ne sont pas
considérées. Elles sont remplacées par zéro.
Lorsque l'on doit déterminer une probabilité à partir de la loi normale, on
essaie de se ramener à une probabilité considérée dans la table.
Quelques cas concrets sont illustrés
ci-dessous
Positionnez le curseur sur un cas pour obtenir l'illustration
correspondante.
Exemples:
Le poids des tomates produites par un jardinier obéit à une loi normale de
moyenne 200 gr et d'écart type 40 gr.
-
Calculez la probabilité que le poids d'une tomate
excède 250 gr.
Solution:
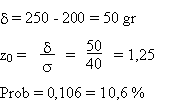
-
Calculez la probabilité que le poids d'une tomate
soit inférieur à 100 gr.
Solution:
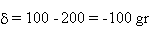
la loi normale est symétrique 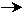 on ne
s'occupe pas du signe on ne
s'occupe pas du signe
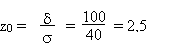
moins de 100 gr: on s'écarte donc de la valeur moyenne
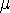 = 200 gr de
plus de z0 = 200 gr de
plus de z0
Prob = 0,006 = 0,6 %
-
Calculez la probabilité que le poids d'une tomate
soit inférieur à 230 gr.
Solution:
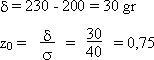
L'intervalle (< 230 gr) considéré contient la valeur moyenne
(200 gr) 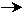 on prend
1 - Prob(table):. on prend
1 - Prob(table):.
Prob = 1 - 0,227 = 0,773 = 77,3 %
-
Calculez la probabilité que le poids d'une tomate
ne s'écarte pas de la valeur moyenne de plus de 20 gr.
Solution: on calcule d'abord la probabilité
que
le poids s'écarte de plus de 20 gr, vers le haut ou vers le bas:
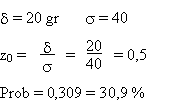
On doit multiplier par 2 car on considère les deux côtés
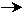 Prob = 2 × 0,309 = 0,618
Prob = 2 × 0,309 = 0,618
On a donc une prob. de 0,618 que le poids s'écarte de
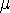 de plus de 20 gr, et donc une
prob. 1 - 0,618 que le poids ne s'écarte pas de plus de
20 gr. de plus de 20 gr, et donc une
prob. 1 - 0,618 que le poids ne s'écarte pas de plus de
20 gr.
Réponse: 0,382 = 38,2 %
3. Forme de la distribution d'échantillonnage
Supposons que nous analysions une population quelconque à partir d'un
ensemble d'échantillons.
Pour chacun de ces échantillons, nous calculons une valeur moyenne
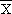 qui est une estimation de la moyenne de la
population qui est une estimation de la moyenne de la
population 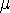 . .
Bien entendu, les estimations 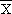 différeront
généralement de la vraie moyenne différeront
généralement de la vraie moyenne 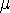 . .
Nous désirons savoir comment les différentes déterminations
 vont se distribuer autour de la vraie
moyenne vont se distribuer autour de la vraie
moyenne 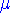
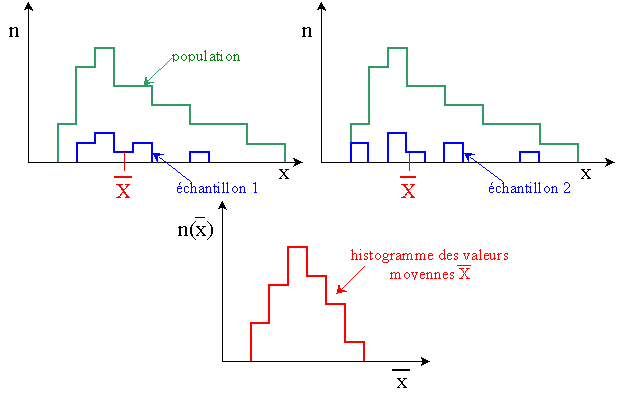
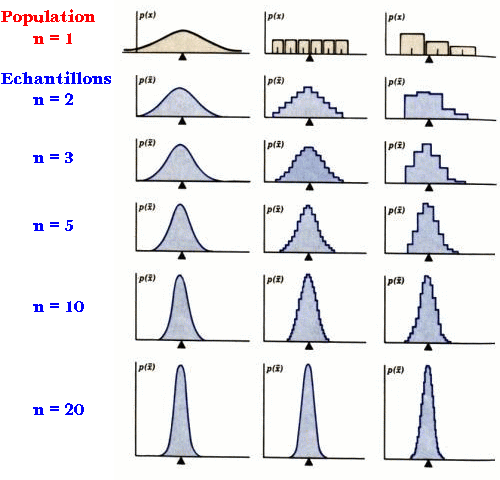
La figure suivante montre l'histogramme des valeurs moyennes
 pour des échantillons de tailles croissantes
tirés des populations indiquées sur la première ligne. pour des échantillons de tailles croissantes
tirés des populations indiquées sur la première ligne.
|
Lorsque la taille de l'échantillon est
suffisamment grande (n  10)
la distribution de la moyenne a une forme
approximativement normale. 10)
la distribution de la moyenne a une forme
approximativement normale.
|
|
L'écart type sur la moyenne est:
Quelle que soit la population sous-jacente, si on utilise des échantillons
suffisamment grands (au moins 10 à 20 individus), la précision de la
valeur moyenne peut être calculée à partir de la loi normale.
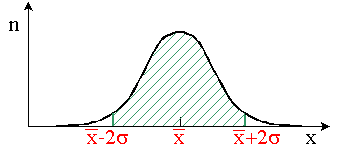
Il y a 68 % ( 2/3) de chances que la
vraie moyenne 2/3) de chances que la
vraie moyenne 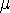 soit dans l'intervalle
compris entre soit dans l'intervalle
compris entre 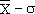 et et 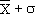 . .
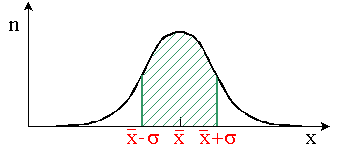
Il y a 95 % de chances que la
vraie moyenne 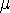 soit dans l'intervalle
compris entre soit dans l'intervalle
compris entre 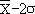 et et 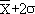 . .
Exemples
-
Une organisation de consommateurs désire savoir si le poids réel des
pains de 800 gr produits dans une boulangerie est bien conforme
au poids annoncé.
Pour cela, elle prélève 100 pains au hasard. Elle obtient un poids moyen
de 780 gr, avec un écart type de 80 gr.
Quelle est la probabilité que le boulanger triche en moyenne sur le
poids de ses pains ?
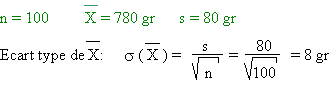
Il n'y a pas tricherie si 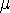 est de
800 gr ou moins, c'est-à-dire 20 gr au-dessus de est de
800 gr ou moins, c'est-à-dire 20 gr au-dessus de
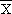 . .
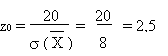
D'après la table, la probabilité que
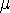 soit supérieur à soit supérieur à
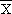 d'au moins 2,5 d'au moins 2,5 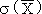 est de 0,006.
est de 0,006.
100 - 100 × 0,006 = 100 - 0,6 = 99,4 %
Il y a 99,4 % de chances pour que le boulanger
triche
 on peut raisonnablement conclure à la
tricherie !
on peut raisonnablement conclure à la
tricherie !
-
Dans une autre boulangerie, l'échantillon de 100 pains conduit au
résultat suivant:
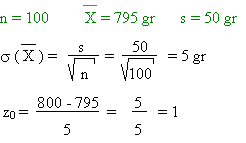
D'après la table, la probabilité que
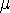 soit supérieur ou égal à
800 gr est de 0,159 soit supérieur ou égal à
800 gr est de 0,159
Il y a donc 84,1 % de chances que ce boulanger triche
Même si il la présomption est forte, ce
n'est pas suffisant pour conclure à la tricherie !
-
Dans une troisième boulangerie, on obtient:
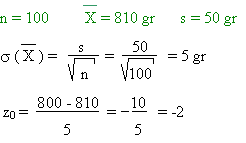
D'après la table, la probabilité que 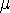 soit inférieur ou égal à 800 gr est de 0,023 soit inférieur ou égal à 800 gr est de 0,023
Il n'y a que 2,3 % de chance que le
boulanger triche.
On peut conclure qu'il est
honnête !
-
Le revenu moyen d'un échantillon représentatif de 16 ménages s'élève à
62 000 F net par mois, avec un écart type de
16 000 F.
-
Quelle est la probabilité que le revenu moyen de l'ensemble de la
population soit inférieur à 60 000 F ?
Solution:
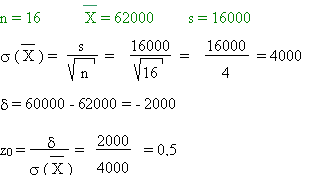
< 60 000: s'écarte de 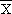 de plus
de 0,5 × de plus
de 0,5 × 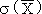
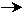 on prend la valeur de la table
on prend la valeur de la table
Prob = 0,309 = 30,6 %
-
Quelle est la probabilité que le revenu moyen de la
population soit inférieur à 65 000 F ?
Solution:
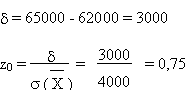
< 65 000: ne s'écarte pas de 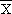 de plus de 0,75 ×
de plus de 0,75 × 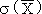 vers
le haut vers
le haut
 on prend la valeur P de la table
et on calcule 1-P on prend la valeur P de la table
et on calcule 1-P
P = 0,227
1-P = 0,773 = 77,3 %
4. Intervalles de confiance
Nous avons vu que la moyenne 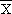 d'un échantillon
aléatoire permet d'estimer la vraie moyenne d'un échantillon
aléatoire permet d'estimer la vraie moyenne
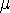 de la population. de la population.
Nous voudrions estimer également la précision de cette moyenne,
c'est-è-dire donner une marge d'erreur ou un intervalle de confiance.
Nous pouvons utiliser les tables de la loi normale pour estimer ces
intervalles de confiance.
En général nous adopterons l'intervalle de confiance è 95 %, soit è
2 ( (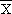 ). ).
Nous pourons donc écrire, soit:
soit, plus explicitement:
Si nous tirons une série d'échantillons de la population, dans 19 cas sur
20 (en moyenne), 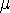 se trouvera dans
l'intervalle de confiance se trouvera dans
l'intervalle de confiance 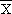 ± 2 ± 2  ( (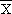 ). ).
Exemples:
-
La taille moyenne d'un échantillon de 51 filles de 2ème
candi. commu. est de 167,9 cm.
L'écart type de cet échantillon est de 5,3 cm.
Si nous supposons que cet échantillon est représentatif de la taille des
filles belges âgées d'une vingtaine d'années, nous pouvons
calculer la taille moyenne de cette population, avec sa marge d'erreur:

Avec 95 % de confiance, nous pouvons donc dire que la taille
moyenne de la population vaut:
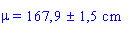
ce qui revient è dire qu'il y a 95 chances sur 100 pour que la taille
moyenne des filles belges de 20 ans se situe entre
166,4 et
169,4 cm.
-
La taille moyenne d'un échantillon de 35 garçons de
2ème candi. commu. est de 182,9 cm.
En supposant de même l'échantillon représentatif, nous pouvons
donner un intervalle de confiance pour la taille des garçons
belges de 20 ans.
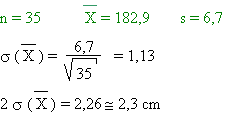
Avec 95 % de confiance, on a donc:
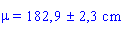
5. Comparaison de deux échantillons indépendants
Des échantillons sont indépendants lorsqu'une
modification dans l'un d'eux n'a pas d'influence sur les autres.
Par exemple, un échantillon de filles et un échantillon de garçons
sélectionnés pour déterminer le poids moyen des filles et celui des
garçons sont indépendants.
Par contre, les personnes qui affirment voter pour un parti A ou pour un
parti B dans un sondage politique ne forment pas deux échantillons
indépendants car si une personne de plus déclare voter pour A, il y a un
électeur potentiel en moins pour B (les résultats de A et B s'influencent).
Si nous avons 2 échantillons indépendants, de moyennes
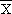 1 et 1 et
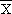 2, avec des écarts types sur ces
moyennes, 2, avec des écarts types sur ces
moyennes,  1( 1(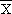 ) et ) et  2( 2(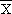 ), nous pouvons estimer la différence des moyennes,
ainsi que l'écart type sur cette différence. ), nous pouvons estimer la différence des moyennes,
ainsi que l'écart type sur cette différence.
La différence moyenne est simplement:
Son écart type est donné par:
(formule approchée, mais suffisamment
précise)
Pour la taille des filles et des garçons, nous obtenons:
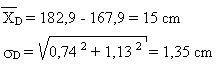
L'intervalle de confiance à 95 % est de:
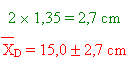
Si nous désirons maintenant répondre à la question suivante:
les garçons sont-ils plus grands, en moyenne,
que les filles ?
-
différence moyenne de taille:
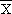 D = 15,0 cm D = 15,0 cm
-
écart type de cette différence:
 D = 1,35 cm D = 1,35 cm
-
nombre d'écarts types au-dessus de 0 cm
(0 cm  pas de différence de
taille) pas de différence de
taille)
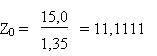
Dans une distribution normale, la probabilité d'avoir une valeur qui
s'écarte de la moyenne de plus de 11  est inférieure à 2.10-28 et donc
complètement négligeable.
est inférieure à 2.10-28 et donc
complètement négligeable.
Si nos échantillons sont représentatifs, il n'y a donc aucune chance que la
différence de taille soit due au hasard.
Sur base de nos échantillons, nous sommes donc pratiquement certains que
les garçons sont, en moyenne, plus grands que
les filles.
Exemple
On sélectionne un échantillon de 25 paysans syldaves. La superficie de leurs
terres s'élève à 24 hectares en moyenne, avec un écart type de 5
hectares.
Pour un échantillon de 16 paysans bordures, la superficie moyenne des terres
est de 26 hectares, avec un écart type de 8 hectares.
Quelle est la probabilité que les paysans syldaves
aient, en moyenne, plus de terres que les bordures ?
Solution:
différence moyenne: (syldave-bordure):
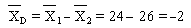
écart type sur la différence:
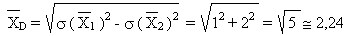
les syldaves ont plus de terre en moyenne que les bordures si la différence
est >0 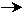 s'écarte de la valeur moyenne calculée
de plus de 2 s'écarte de la valeur moyenne calculée
de plus de 2
table 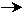 Prob = 0,187 = 18,7 % de chances que la superficie
moyenne soit supérieure en Syldavie.
Prob = 0,187 = 18,7 % de chances que la superficie
moyenne soit supérieure en Syldavie.
6. Comment arrondir ?
Il n'y a pas de recette absolue pour arrondir correctement.
Arrondir trop peut entraîner une perte de précision.
Arrondir trop peu suggère une précision illusoire et diminue la
lisibilité des résultats.
La recette suggérée ci-dessous est un bon compromis entre les deux
extrêmes.
Pour éviter de perdre de la précision, surtout dans les longs calculs,
il est conseillé de n'arrondir qu'à la fin, lors de la présentation des
résultats.
-
Sur la marge d'erreur (en
général,  ):
garder 2 chiffres significatifs. ):
garder 2 chiffres significatifs.
C'est-à-dire, en partant de la gauche, le premier chiffre différent de
0 et le suivant.
Le dernier chiffre significatif que l'on garde est
arrondi vers le bas ou le haut pour que la valeur arrondie soit la plus
proche de la valeur calculée:
vers le bas si le chiffre suivant est 0,1,2,3 ou 4;
vers le haut si le chiffre suivant est 5,6,7,8 ou 9;
Exemples:
 |
arrondi correct |
35,2438
2379
0,6694
0,0023256
0,0004041
0,89712
|
35
2400
0,67
0,0023
0,00040
0,90
|
-
Sur le résultat affecté d'une certaine marge
d'erreur  :
garder le même nombre de décimales
que pour :
garder le même nombre de décimales
que pour  . .
Exemples:
résultat |
 |
résultat arrondi |
1864,387
0,68088
24,52698
2624,57
54867,12
|
6,8
0,013
0,25
120
2000
|
1864,4
0,681
24,53
2620
54900
|
(Dans le dernier cas, le chiffre des centaines de
 est significatif car, bien que 0, il suit le
premier chiffre non nul). est significatif car, bien que 0, il suit le
premier chiffre non nul).
Exercices d'arrondi
Arrondissez correctement les résultats suivants, ainsi que leurs marges
d'erreur.
7. Exercices
-
Application n°1
-
Application n°2
|
Un client commande des barres métalliques
de 12 m de long. Il tolère une erreur maximale de 5 mm.
L'usine A produit des barres dont la
longueur suit une distribution
normale de moyenne 12 m et d'écart type 4 mm.
L'usine B produit des barres dont la
longueur suit une distribution
normale de moyenne 12,001 m et d'écart type 4 mm.
Calculez la fraction des barres qui seront rejetées par le client, au
départ des deux usines.
|
|
Chapitre:
1
2
3
4
5
6
7
|





