|
1. Corrélation entre deux variables
Jusqu'à présent, nous nous sommes intéressés à des questions du type:
-
quelle est la taille moyenne des garçons belge âgés d'une vingtaine
d'années ?
-
quelle est la probabilité pour qu'un médicament soit efficace ?
-
quel pourcentage de voix un parti politique recueillera-t-il aux
prochaines élections ?
-
quelle fraction des barres métalliques produites par une usine
sera-t-elle rejetée par le client ?
-
le poids moyen des pains produits dans une boulangerie est-il supérieur à
800 grammes ?
Dans toutes ces questions, nous étudions le comportement statistique d'une
seule variable:
taille, efficacité du médicament, pourcentage de
voix, longueur des barres, poids des pains.
Il existe cependant toute une gamme de problèmes statistiques où l'on
s'intéresse à la relation entre plusieurs
variables.
Exemples:
-
les individus les plus grands sont-ils les plus lourds ?
-
le revenu d'une famille a-t-il une influence sur les résultats scolaires
des enfants ?
-
y a-t-il une relation entre le tabagisme et les cancers du poumon ?
-
le rendement en céréales dépend-il de la quantité d'engrais
utilisée ?
-
la productivité d'une entreprise est-elle liée au salaire des ouvriers ou
employés ?
Dans ces questions, nous désirons savoir si le comportement d'une variable
est influencé par la valeur d'une autre variable:
taille |
 | poids |
tabagisme |
 | cancer |
revenu |
 | résultats |
rendement |
 | engrais |
La relation peut être causale ou non.
Pour étudier les relations ou
corrélations entre deux variables
statistiques, on peut les porter sur un graphique.
Exemple:
Relation entre la taille et le poids des individus.
Pour chaque individu de l'échantillon, on porte sur un graphique:
chaque individu est donc, dans ce graphique,
représenté par un point
(point représentatif).
Soit un individu mesurant 172 cm
et pesant 66 kg:
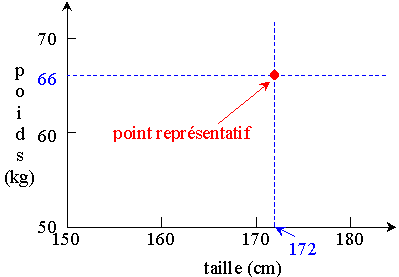
Dans le graphe, il y aura donc autant de points qu'il y a d'individus dans
l'échantillon.
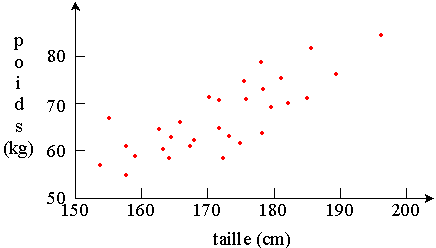
Relation entre le poids et la taille dans un échantillon de 30
individus.
On peut (par la pensée ou réellement) tracer une droite qui passe au mieux
par ces points (au milieu du "nuage" de points).
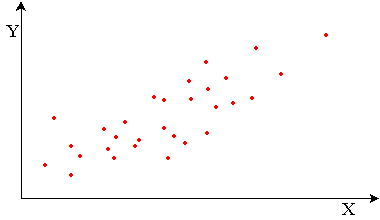
Si cette droite "monte", on dira qu'il y a
corrélation positive entre les deux
variables.
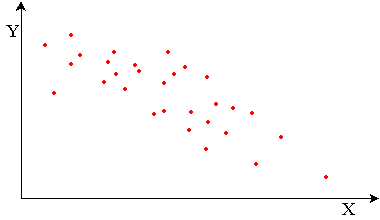
Si elle "descend", c'est une
corrélation négative.
Si elle est "horizontale", ou si on ne peut
pas décider, c'est qu'il y a absence de
corrélation.
Corrélation positive:
Corrélation négative:
Absence de corrélation:
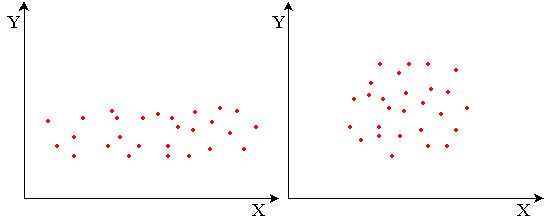
La qualité de la corrélation entre deux
variables peut se mesurer par la dispersion
des points autour de la relation moyenne.
Corrélation parfaite:
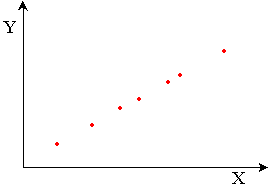
Bonne corrélation (corrélation forte):
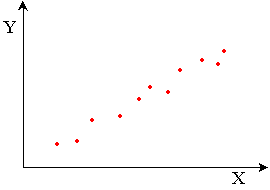
Mauvaise corrélation (corrélation faible):
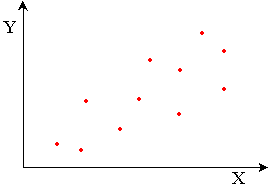
Exemples:
-
Corrélation entre le poids et la taille pour les garçons de
2ème candidature communication (1998).
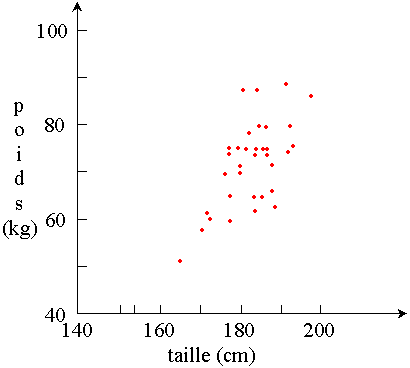
On constate une augmentation du poids avec la taille
(corrélation positive): les garçons
les plus grands sont généralement les plus lourds.
Mais la dispersion des points est assez grande:
la corrélation est assez faible.
-
Corrélation entre le poids et la taille pour les filles de
2ème candidature communication (1998).
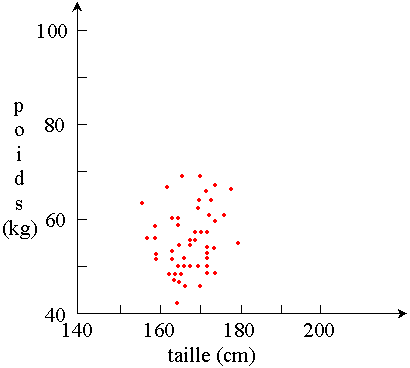
On ne constate pas de relation entre du poids et la taille
(abscence de corrélation):
le poids des filles est pratiquement indépendant de leur taille.
(les filles les plus grandes sont donc les plus minces)
2. Méthode des moindres carrés
Si on se contente de tracer à main levée la droite qui "passe au mieux"
par les points représentatifs, différentes personnes vont obtenir des
résultats différents.
Il existe une méthode mathématique pour déterminer la "meilleure"
droite: c'est la méthode des moindres
carrés.
Elle consiste, dans sa version la plus simple, à trouver la droite
qui minimise les carrés des écarts des points représentatifs à cette
droite.
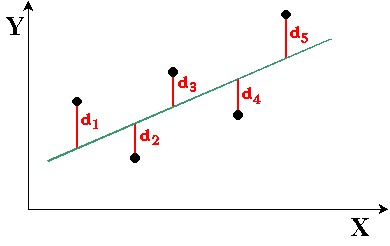
Trouver la droite telle que la somme des carrés des écarts d1,
d2,... soit
minimale:
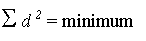
Soit:
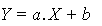
l'équation de la droite cherchée (droite
de régression).
Les coefficients a et
b peuvent être calculés à partir
des formules suivantes:
Pente:
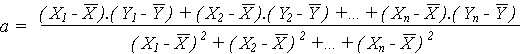
ou
Ordonnée à l'origine:
Rappels:
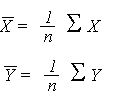
3. Coefficient de corrélation
Le signe de la pente a donne le sens de
la corrélation, mais pas sa qualité.
a > 0 |
corrélation positive |
a < 0 |
corrélation négative |
a = 0 |
pas de corrélation |
La qualité de la corrélation peut être
mesurée par un coefficient de corrélation
r.
Le coefficient de corrélation est compris entre
-1 et +1.
Plus il s'éloigne de zéro, meilleure est la corrélation.
r = +1 |
corrélation positive parfaite |
r = -1 |
corrélation négative parfaite |
r = 0 |
absence totale de corrélation |
Quelques exemples de corrélation
(le coefficient de corrélation r est indiqué dans chaque cas
Exemples:
-
Supposons un échantillon aléatoire de 4 firmes pharmaceutiques présentant
les dépenses de recherche X et les profits Y suivants (en millions de
dollars)
Trouvez la droite de régression et le coefficient de corrélation.
Calculons tout d'abord 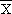 et et
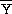
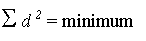
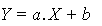
Complétons le tableau suivant:
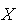 |
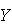 |
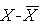 |
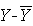 |
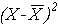 |
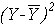 |
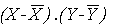 |
40
40
30
50
|
50
60
40
50
|
0
0
-10
+10
|
0
+10
-10
0
|
0
0
+100
+100
|
0
+100
+100
0
|
0
0
+100
0
|
On a donc:
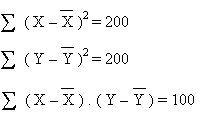
Les coefficients de la droite de régression sont:
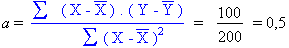
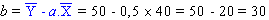
Et le coefficient de corrélation:
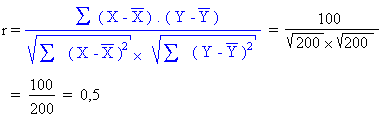
La corrélation est positive et de
qualité moyenne
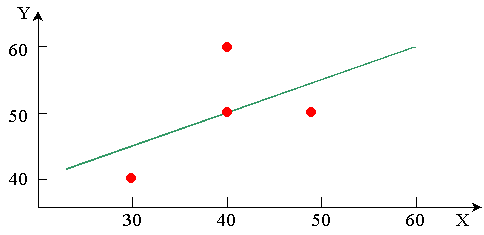
-
La corrélation entre la taille (X) et le poids (Y) pour les garçons
de 2ème candi. commu. donne les résultats suivants:
(a)
|
droite de régression: Y = a X + b
a = 0,816 b = -77,0 |
(b)
|
coefficient de corrélation
r = 0,61 |
La corrélation est donc positive, de
qualité moyenne
-
De la même manière, pour les filles, on obtient:
(a)
|
droite de régression: Y = a X + b
a = 0,239 b = 16,6 |
(b)
|
coefficient de corrélation
r = 0,20 |
La corrélation est positive (les filles les
plus grandes tendent à être les plus lourdes), mais de
très mauvaise qualité (r proche de
zéro).
Remarques:
-
Le coefficient de corrélation nous donne des informations sur
l'existence d'une relation linéaire (sous
forme d'une droite) entre les deux grandeurs considérées.
Un coefficient de corrélation nul ne signifie pas l'absence de toute
relation entre les deux grandeurs. Il peut exister une relation
non linéaire entres elles.
(cf. exemple (f) ci-dessus: la connaissance de X nous donne des
informations sur la valeur de Y).
-
Il ne faut pas confondre corrélation et
relation causale.
Une bonne corrélation entre deux grandeurs peut révéler une relation
de cause à effet entre elles, mais pas nécessairement.
Exemples:
-
Si on compare la durée de vie des individus à la quantité de
médicaments pour le coeur qu'ils ont absorbée, on observera
probablement une corrélation négative. Il serait imprudent de
conclure que la prise de médicaments pour le coeur abrège la vie des
individus
(en fait, dans ce cas, la corrélation est l'indice d'une cause
commune: la maladie de coeur).
-
Le soleil tire son énergie de réactions nucléaires transformant
l'hydrogène en hélium. Notre société tire une bonne part de son
énergie de la combustion du pétrole. Si on compare, année après
année, la quantité d'hélium contenue dans le soleil au prix moyen du
pétrole, on obtiendra une bonne corrélation positive, sans qu'il y
ait la moindre relation de cause à effet, ni aucune cause commune.
-
Depuis une dizaine d'années, la taille de mon fils cadet, né en
1989, est très bien corrélée avec la puissance de calcul des
ordinateurs personnels. Cette excellente corrélation ne révèle bien
évidemment aucune relation de cause à effet, ni cause commune.
L'existence d'une corrélation, aussi bonne soit elle, n'est jamais
la preuve d'une relation de cause à effet.
Chapitre:
1
2
3
4
5
6
7
|





